
Le Rubik’s Cube
1/ Tracé de la perspective :fuyantes, point de fuite et ligne d’horizon
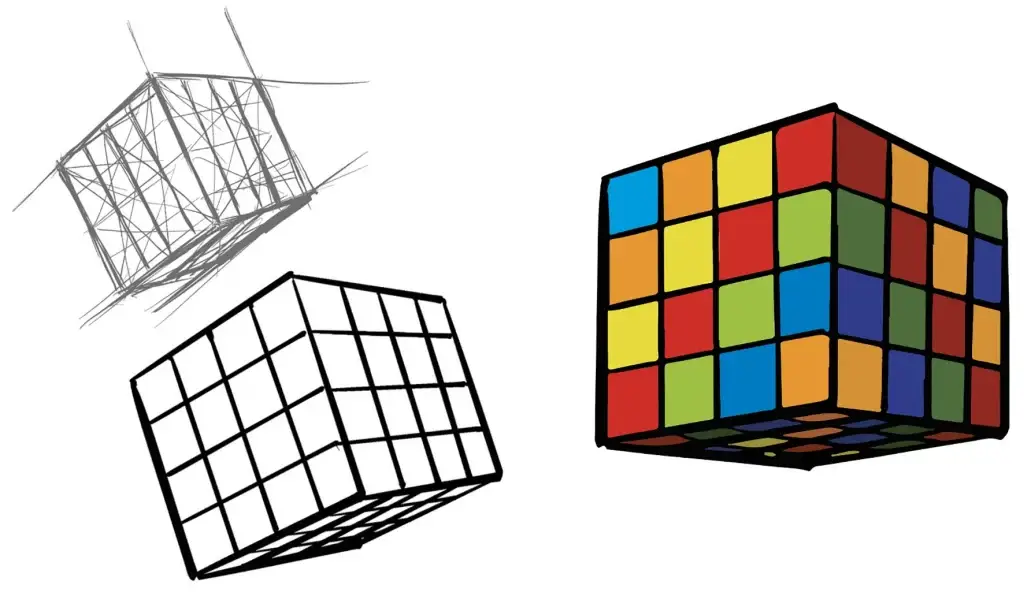

Schéma 1
À partir du cube dessiné précédemment (croquis préparatoire), tracer un repère au niveau de la jonction des 2 faces A et B du cube. Il est important de bien tenir compte de la hauteur des faces du cube dessiné sur le croquis préparatoire. Le repère tracé en rouge sera nommé “arête“. À partir de la face gauche du cube (A), tracer sa ligne supérieure et sa ligne inférieure jusqu’à ce qu’elles se croisent et forment un point d’intersection que l’on nommera “Point de fuite 1”. Nous nommerons ces lignes “Fuyantes 1 et 2”.


Schéma 2
Nous allons maintenant déterminer le deuxième point de fuite (Point de fuite 2 ou PF2) à partir des fuyantes que l’on nommera “Fuyantes 3 et 4”. Les 2 points de fuite symbolisés par des points oranges vont être reliés ensemble et formeront ainsi “La ligne d’horizon”. Cette ligne est importante car elle sert de repère principal par rapport à la hauteur de vue du spectateur.

Des différences de tracés peuvent apparaître entre le croquis initial du cube et sa construction (cf. schéma 2).
2/ Étude de développement de la face gauche du cube

Schéma 3

Il faut calculer la largeur de la face gauche du cube (A). Des règles de construction rigoureuses sont à respecter. La largeur de 2 carreaux servira comme repère, symbolisé par deux traits rouges.

Schéma 4

La largeur de 2 carreaux ainsi définie, nous relions les deux traits rouges afin de former un rectangle en perspective.

Schéma 5

À partir des angles du rectangle, nous traçons 2 diagonales : la première partira de l’angle supérieur gauche (A) pour aller vers l’angle inférieur droit (B) et la seconde débutera de l’angle supérieur droit (C) vers l’angle inférieur gauche (D). À l’intersection de ces diagonales se forme un point E sur lequel nous dessinons une ligne centrale en direction du point de fuite “PF1”.

Schéma 6

La ligne centrale tracée est important car elle va nous servir à déterminer la deuxième partie de la face gauche du cube. Pour cela, nous allons partir de l’angle supérieur droit du rectangle (B). Nous tracerons une nouvelle diagonale qui passera par le milieu du côté gauche du rectangle et qui définira un nouvel angle appelé D’ ; le milieu du côté gauche étant déterminé par la ligne centrale.

Schéma 7

La diagonale tracée a créé un point D’ situé au nouvel angle inférieur gauche du cube. Pour définir l’arête gauche du cube, nous allons tracer un repère symbolisé par un trait rouge partant du point D’.

Schéma 8

Maintenant, il ne reste plus qu’à tracer l’intégralité du contour de la face gauche du cube qui comprendra l’intégralité des angles.
3/ Étude de développement de la face droite du cube

Schéma 9

Nous allons maintenant nous intéresser à la face droite du cube (B). La réalisation est similaire à l’étape 2 (cf. schémas 3 à 8). Nous prenons en compte la largeur de 2 carreaux sur la face gauche du cube que nous reportons sur le côté droit.

Schéma 10

Nous relions ensuite les deux repères rouges afin que cela forme un rectangle en perspective.

Schéma 11

À partir des angles du rectangle, nous traçons 2 diagonales : la première partira de l’angle supérieur droit (F) pour aller vers l’angle inférieur gauche (I) et la seconde débutera de l’angle supérieur gauche (G) vers l’angle inférieur droit (H). À l’intersection de ces diagonales se forme un point K sur lequel nous dessinons une ligne centrale en direction du point de fuite “PF2”.

Schéma 12

La ligne centrale tracée est importante car elle va nous servir à déterminer la deuxième partie de la face droite du cube. Pour cela, nous allons partir de l’angle supérieur gauche du rectangle (F). Nous traçerons une nouvelle diagonale qui passera par le milieu du côté droit du rectangle et qui définira un nouvel angle appelé I’ ; le milieu du côté droit étant déterminé par la ligne centrale.

Schéma 13

La diagonale tracée a créé un point I’ situé au nouvel angle inférieur droit du cube. Pour définir l’arête droite du cube, nous allons tracer un repère symbolisé par un trait rouge partant du point I’.

Schéma 14

Maintenant, il ne reste plus qu’à tracer l’intégralité du contour de la face droite du cube.


Schéma 15

Nous allons maintenant développer la face située en dessous du cube. Pour cela, nous allons tracer une nouvelle fuyante que l’on nommera “Fuyante 5”, partant de l’angle inférieur droit du cube (I’) se dirigeant vers le “Point de fuite 1”. Même procédure pour l’angle inférieur gauche (D’) avec une fuyante que l’on nommera “Fuyante 6”, qui se dirigera vers le “Point de fuite 2”.

Schéma 16

Le croisement des fuyantes “2 / 4 / 5 / 6” formera le contour de la face en dessous du cube.
4/ Mise en valeur des faces du cube par la lumière

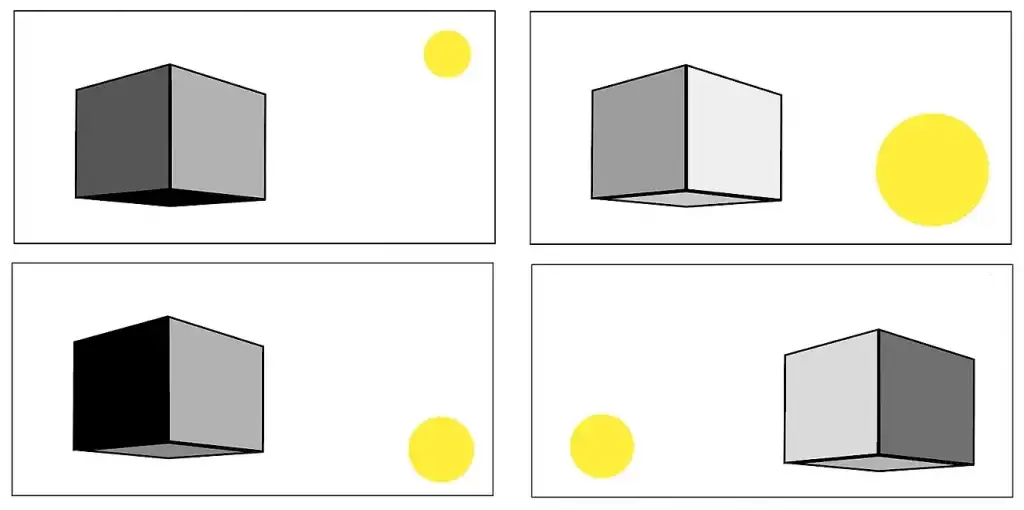
Schéma 17

Avant de développer les facettes qui viendront se positionner sur les faces du cubes, nous allons observer dans un premier temps la réaction d’une source lumineuse venant de l’arrière gauche par rapport au cube.
5/ Définition des facettes sur les faces du cube

Schéma 18

Pour définir les facettes situées sur les faces du cube, il faut tracer les diagonales des faces 1, 2 et 3.

Schéma 19

Chaque diagonale part d’un angle pour atteindre l’angle opposé. L’intersection des diagonales délimitera les axes centraux gauches et droites qui seront définis en fonction des lignes et points de fuite (PF1 et PF2).

Schéma 20

Il s’agit maintenant de diviser en deux les parties 1, 2, 3 et 4 afin de définir les axes centraux et verticaux de chaque partie. Nous utiliserons la technique des diagonales croisées pour trouver le centre des surfaces.

Schéma 21

Il s’agit maintenant de diviser en deux les parties 5, 6, 7 et 8 afin de définir les axes centraux et horizontaux de chaque partie. Comme lors de l’étape précédente, les diagonales croisées permettront de trouver le centre des surfaces.

Schéma 22


Schéma 23

Il s’agit maintenant de diviser en deux les parties 9, 10, 11 et 12 correspondant à la face du dessous du cube. Dans ce cas, contrairement aux étapes précédentes où nous avons utilisé les diagonales pour calculer le milieu des surfaces, nous allons prendre en compte les repères des cases calculés précédemment (flèches bleues). Les axes ou fuyantes correspondant à ces repères se projettent sur les points de fuite PF1 et PF2.

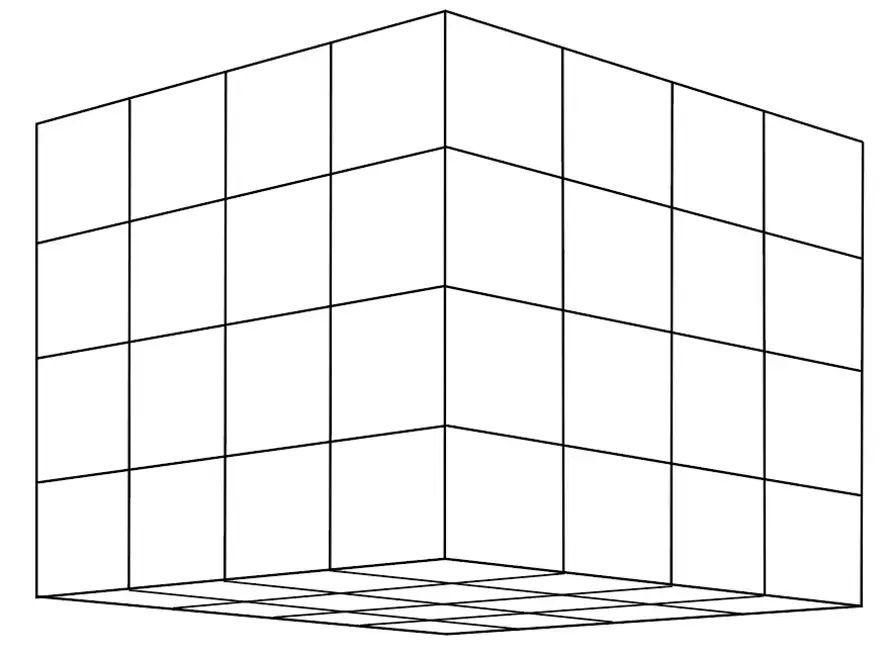
Schéma 24

Notre cube est maintenant terminé. Sa construction tient compte des règles rigoureuses de la perspective. Nous allons passer à l’étape de la mise en couleurs.
6/ Mise en couleurs du cube “Rubik's Cube”

Schéma 25

Article rédigé par Vincent Couppey, Artiste-Peintre /Atelier Impression’Art / 11 octobre 2025
© Vincent Couppey 2025 – Tous droits réservés
